
A-Level Maths Preparation 2019/20 – The Plan
The plan is simple. You need to spend 2-3 hours a week doing some additional A-Level Maths preparation. The keyword is ‘additional’, which means that this doesn’t include the time you spend doing maths at school! Your time needs to be spent resourcefully.
Below is a list that should give you ideas on how to spend your time when studying:
- Examples – Do as many as you can, and don’t shy away from re answering a question you’ve done before. Practice makes perfect. You should use examples from relevant textbooks and past exam papers. P.S. don’t do all the ‘easy’ examples at the beginning of each exercise and avoid these with the ‘E/P’ sign.

You and I both know that you’re more likely to get a question like this in your exam than.
‘Factorise x2-1′
- Periodically read your course spec – This is so important! In a way, it literally tells you what they can test you on. I also use it to identify links between topics. Below is part of a course spec that I scratched from AQA website.

Remember the A-Level Maths Course Specs
When I see the word ‘links’, I usually underline it. This tells me that examiners are perfectly capable of asking me questions about histograms, binomial distribution and even points of inflection in a ‘Normal distribution question‘. So when I study about normal distribution, I need to research how it relates to these other topics and look for relative past exam questions. I highly recommend you start doing this.
Click below for course specs:
Watch videos – There are 1000’s of YouTube videos out there which do a great job of explaining your problem topics. During the year, we’ll be creating and recommending several videos which will help you to further understand them. Exam Solutions, by Stuart Sidders, is the guy I heavily recommended. I have used his video content to help me throughout my academic career including A-Level Mathematics and Calculus at University. I find his content and approach is phenomenal. Does domain and range of functions ever confuse you? Watch this video.
Watch videos
There are 1000’s of YouTube videos out there which do a great job of explaining your problem topics. During the year, we’ll be creating and recommending several videos which will help you to further understand them. Exam Solutions, by Stuart Sidders, is the guy I heavily recommended. I have used his video content to help me throughout my academic career including A-Level Mathematics and Calculus at University. I find his content and approach is phenomenal. Does domain and range of functions ever confuse you? Watch this video
As you can see, his video tutorials are nice and short (generally about 10 minutes). They cover the foundations of each topic as well as exam questions which have varying levels of difficulty. His approach and delivery is methodical, rigorous and highly effective. Even better, he is constantly renewing his content to make it relevant to the Edexcel, AQA and OCR syllabus. Surely that’s what you want, right? A quick and easy way to digest new information. If you’re doing A-Level Mathematics, I would definitely keep an eye out for these videos. They are some of the best FREE material on the net!
– – – A-level Maths Tuition – – –
Air Maths Tuition – The Plan

Every day after school, we’ll be going through all the topics in you’re A-Level and IB and Foundation Mathematics curriculum for an hour. These topics will include proofs, binomial expansion, sequences and series, integration, numerical integration etc.
I have plenty of experience in this field and will be covering these topics in great depth, helping you to recognise and answer a wide array of question types.
So, if you ‘don’t get it’ at school, odds are that you will in our lessons. You can learn more about how our lessons work by clicking on this link.
We’ll be uploading homework every week into your student dashboards for you to complete and solidify your understanding of the work. We try to get you thinking about exam-style questions as early as possible and this is reflected in the homework.
– – – A-level Maths Tuition – – –
A-Level Maths Preparation Preseason
So, ready to start?
Not just yet. Before we get started, there are 2 essentials you’ll need to lock down or at least refresh yourselves with.

These are:
- AS prerequisites
- The basics
AS prerequisites
Due to the scope of work at AS Level, I wouldn’t attempt to revise it all now for two reasons:
a) it’s too long
b) it’s not entirely necessary. This is because several topics such as differentiation, trigonometry and integration are revisited in far greater depth in year 2 A level Mathematics.
However, the AS prerequisites that I would refresh are:
- Polynomial functions – Degrees, finding roots, equating coefficients, completing the square, discriminant.
- Geometry – Graphs, straight lines, circles, shape properties (angles, parallel lines, areas)
- Logarithms – Law of logarithms, solving logarithmic equations
- Indices – Law of indices
- Surds
- Trigonometry – SOHCAHTOA will help for vectors, projectiles and forces in Mechanics this year.
- Probability
- Mathematical notation learnt at AS level – AQA has a pretty neat table in Appendix A, which defines the notation you should already be familiar with.
These are the AS prerequisites that show up the most in Year 2.
– – – A-level Maths Tuition – – –
The Basics
If you don’t master the basics, I guarantee that these will haunt and hurt you this year. Here are a few which creep up all the time
B I D M A S
From my experience, this is probably the number one biggest bogey for students.
In case you’ve forgotten, BIDMAS is just an acronym which helps you know which order to perform your operations. It stands for Brackets, Indices, Division, Multiplication, Addition, and Subtraction.[/vc_column_text][vc_column_text]Examples-
1)
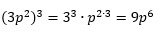
After seeing that you can’t simplify or evaluate what’s inside the brackets, you can then use indices.
2)

If you rewrite
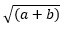
as
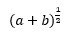
You will realise that square root belongs to the family of indices.
And remember, it’s bracketed 1st and then indices!
3)
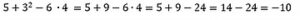
4)
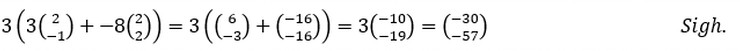
BIDMAS really doesn’t need to be an issue at this level as you’ll have much bigger fish to fry this year. So practice now!
– – – A-level Maths Tuition – – –
The difference of two squares
This is another one that haunts regularly. You may need to use this method to factorise, simplify expressions or prove trigonometric identities. But first, you need to recognise it.
Definition
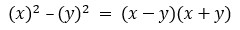
Basically, any two square numbers that are subtracted from each other can be factored as follows:
Examples:
1)
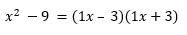
2)
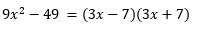
3)

Notice that the constant terms of the RHS are square roots of the LHS. See the pattern now?
Thanks to Maths Guru Jo Morgan who recently brought my attention to a new way of factorising quadratic equations. Although the method isn’t meant to be pretty, I appreciate it as it drums home the importance of recognising the difference of 2 squares. Try to see if you can work out which line it is applied to here.
– – – A-level Maths Tuition – – –
Fractions
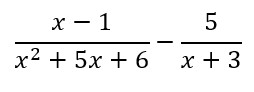
You’ll be dealing with a lot of questions that look like this:
So, you’ll need to know how to perform all operations with fractions that have different denominators, whole numbers and fractions, mixed numbers, nested fractions etc.
In case you’ve forgotten, humbly watch these videos.
Adding fractions with a different denominator
Subtracting fractions with a different denominator
Dividing fractions and Mixed numbers
The kind of things students struggle with are:
Examples –
Whole numbers and fractions-
1)
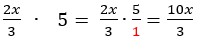

Just make it clear what’s in the numerator and what’s in the denominator and you’ll be fine.
Nested fractions –
3)
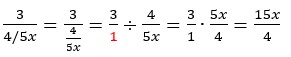
– – – A-level Maths Tuition – – –
Intersection points and asymptotes
This year, we’ll be regularly studying graphs of things called ‘parent functions’ and seeing how they can be transformed. Examples of parent functions are:
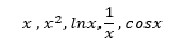
You need to get into the habit of calculating and plotting where a graph crosses the axes (x and y-intercepts). You also need to be able to determine undefined regions in any function. These are called ‘asymptotes’.
Intercepts and asymptotes are massively important as they serve as a great point of reference and help you to transform graphs and calculate domain and range.
Fear not – we’ll go though plenty of examples in our live lessons.
Conclusion
If you don’t master the basics, you’ll surely get stuck often in this course. My advice is to take the humble approach and do some practice to warm yourself up for the year.
Now you’ve looked at the basics and refreshed yourself with the AS prerequisites, I think you’re now ready for a challenging but ultimately rewarding year ahead. See you on the other side.